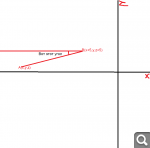
Даны точки A с координатами (x, y, z) и B с координатами (x', y', z').
Для того чтобы узнать указанный в рисунке угол (α) нужно сперва транспонировать одну точку на ту же координату Z, узнать расстояние между ними (получится картезианский план X-Y).

При помощи теоремы Пифагора узнаем расстояние между точками B' и B.
Оно равно: d =
sqrt(sqr(x'-x) + sqr(y'-y)). На нашем рисунке длина сегмента [AB'], то есть |AB'| = d.
Также, можно легко узнать расстояние между точками B и B', |BB'| = z' - z;
Узнаем тангенсу,
tan = |BB'|/d = (z' - z)/sqrt(sqr(x'-x) + sqr(y'-y)).
Угол α будет равен
α = arctan(tan) = arctan((z' - z)/sqrt(sqr(x'-x) + sqr(y'-y))).
Согласно идентификаторам функций СА-МПа (чья документация как обычно отсутвует - а точнее документация функции
atan), функция будет такова:
PHP код:
Float:alfa = atan((z1 - z)/sqrt(sqr(x1-x) + sqr(y1-y))); //где x, y, z - координаты первой точки, а x1, y1, z1 - координаты второй.



 Ответить с цитированием
Ответить с цитированием